When playing around with memory management a matrix multiply is often mentioned as a TLB thrasher, and a good way to stress your system. It's interesting to illustrate this process a little.
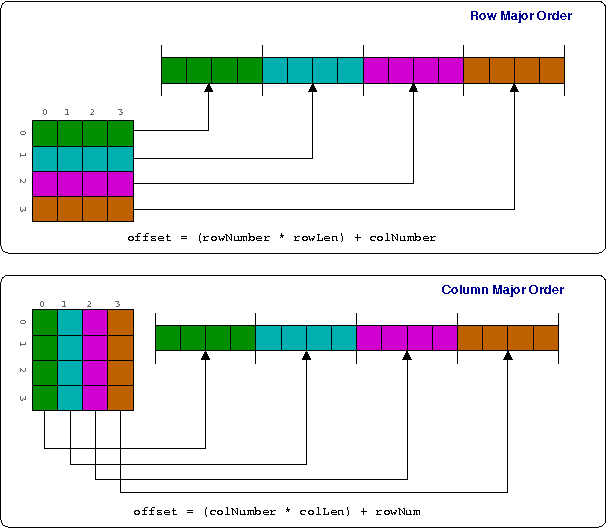
The first thing to remember is that C99 (6.5.2.1 to be precise) dictates that arrays are always stored in row-major order, as shown below.
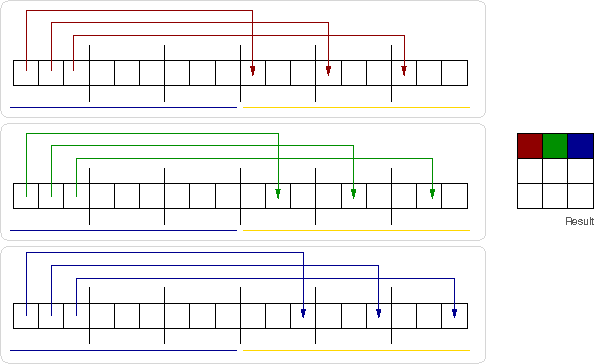
So, remembering back to first year algebra, to multiply two matrices we multiply and sum rows and columns, illustrated linearly as the computer see it below. Black lines are page boundaries, while boxes are matrix elements.
The simplest code to do this is usually along the lines of
int a[LEN][LEN];
int b[LEN][LEN];
int r[LEN][LEN];
int i,j,k
for(i=0; i < LEN; i++)
for(j = 0; i < LEN; j++)
for(k = 0; k < LEN; k++)
r[i][j] += a[i][k] + b[k][j];
We can see how we have a repeated linear walk over the memory holding matrix b, done for each element in a. If we make b sufficiently large (say, a few hundred pages) we can be sure that by the time we get to the end, we have kicked out the earlier TLB entries. Then we start all over again, and start faulting pages back in. Thus a matrix multiply problem comes down to doing repeated page-sized stride walks over a linear region.
Looking at the diagram, it is also clearer what can solve this problem. We can either have more TLB entries, so we don't have to kick out entries which we will use again, or have larger pages -- e.g. less black lines. Or a smarter algorithm ...